Achieve a smooth and precise pick & place through PID tuning
PID Tuning of Axis 5
1) Create a test program (Blockly)
Move axis 5 between two angles (e.g., −1.0 rad ↔ +1.0 rad). Create a Blockly program and name it “PID_tuning”.
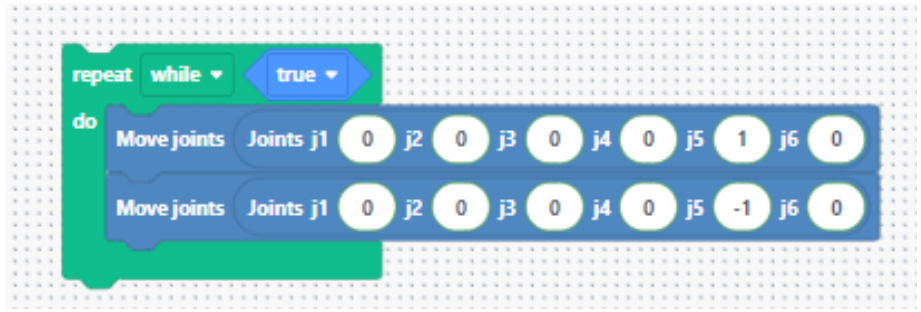
2) Open the PID parameters
In NiryoStudio: My Robot → Settings → Edit PID.

Adjust the gains P, then I, then D. After each change, run the PID_tuning program and observe the plots.
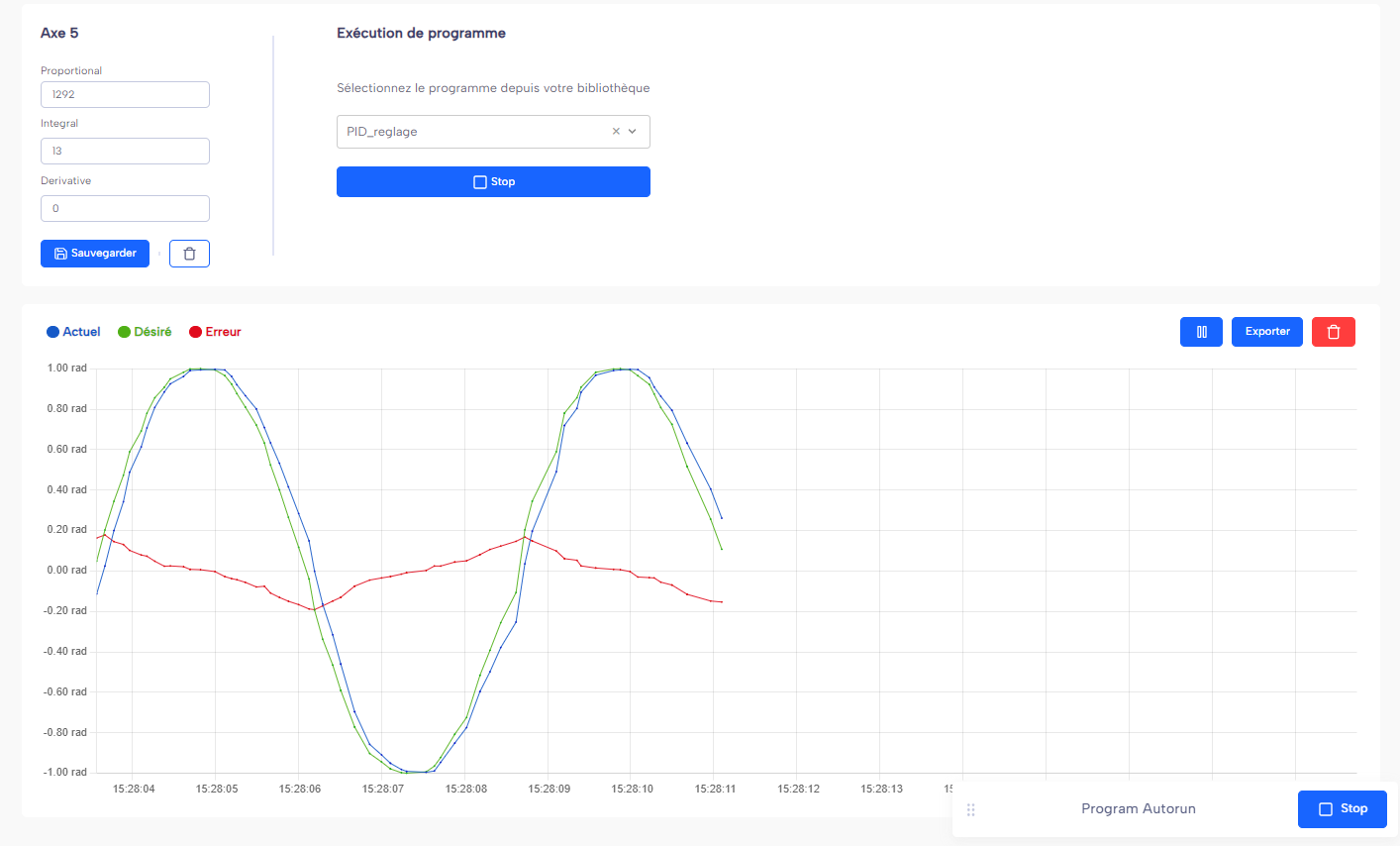
3) What to look for on the plots?
- Speed (rise time) without overshoot.
- Fast stabilization (error → 0).
- No oscillations or visible vibrations.
Example configurations (theoretical)
| P | I | D | Type | Observed behavior |
|---|---|---|---|---|
| 1200 | 400 | 300 | ✅ Stable | Balanced motion |
| 800 | 700 | 200 | ✅ Stable | Accurate, but slow response |
| 2500 | 1000 | 0 | ⚠️ Unstable | Overshoot, oscillations |
| 100 | 2000 | 0 | ⚠️ Unstable | Integral windup, delayed response |
| 3000 | 0 | 0 | ⚠️ Unstable | Purely proportional response, abrupt jumps |
⚠️ These values are indicative for analysis. Each load may require adjustment.
Guided interpretation of tests
Test on gain P
Configuration: P = 3000, I = 0, D = 0.
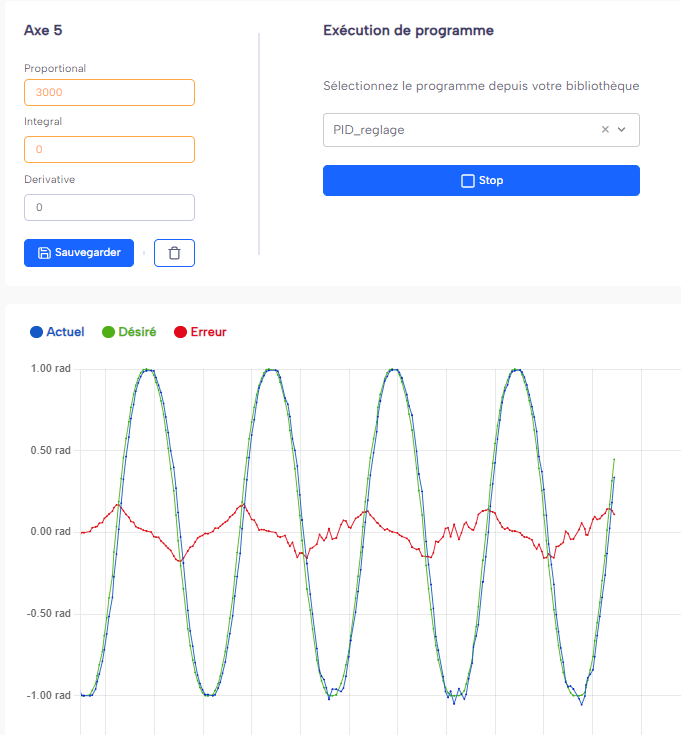
In this test, the proportional gain (P) was significantly increased to 3000, while the integral (I) and derivative (D) gains were set to zero. The blue curve (actual position) closely follows the green curve (desired command), with a relatively small and stable red curve (error). This shows that the system reacts quickly to deviations.
However, a high P value often causes instability or visible shaking, especially in real mechanical systems. Even if it is not obvious on the graph, in practice one can observe vibrations or jerky movements, as the robot corrects even the smallest error too aggressively. Therefore, it is crucial to find a compromise: a P high enough to follow the command properly, but not so high that it triggers overreactions.
Test on gain I
Configuration: P = 200, I = 1200, D = 0.
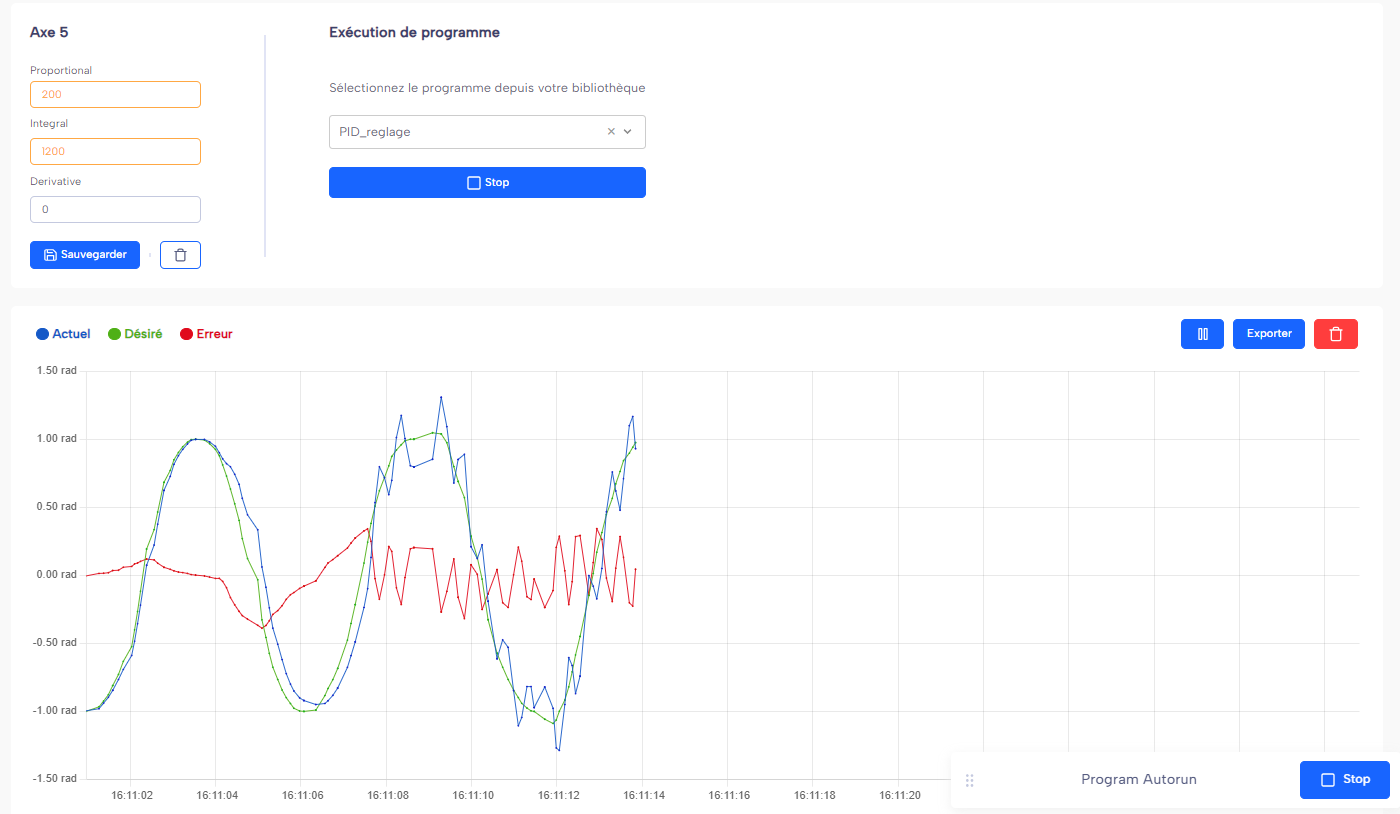
In this example, the integral gain (I) was significantly increased to 1200, while the proportional gain (P) was reduced to 200, and the derivative (D) remained at zero. The red curve representing the error becomes persistent and oscillates around a non-zero value. This occurs because the integral term accumulates the error over time; if too large, it can create slow oscillations or instability. The system takes longer to follow the desired command (green curve), and the gap with the actual position (blue curve) remains visible, especially during direction changes.
Test on gain D
Configuration: P = 100, I = 0, D = 3000.
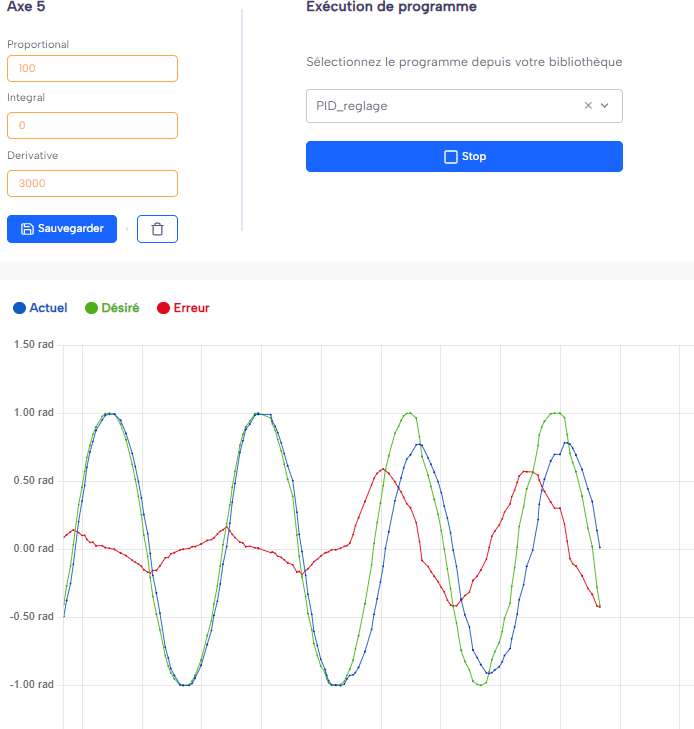
Here, a change in parameters was made during motion: the derivative gain (D) was strongly increased to 3000, while the proportional gain (P) was reduced to 100. This configuration causes a noticeable delay between the blue curve (desired command) and the green curve (actual axis position). This delay indicates a slower response, increasing the error between the command and the reached position.
Interpretation memo
- P ↑ → faster response, but risk of overshoot or oscillations.
- I ↑ → eliminates static error, but may cause windup.
- D ↑ → reduces overshoot, but slows down response.
Your mission: reach clear criteria
- A fast motion without overshoot.
- Quick stabilization (error → 0 in a short time).
- No visible oscillations or vibrations.
Suggested tuning procedure (heuristic):
- Start with
P ≈ medium,I = 0,D = 0. Increase P until the first oscillations appear, then reduce it by ~10–20%. - Add a small amount of D to eliminate overshoot and stabilize.
- Gradually introduce I to remove residual error, while watching for windup.
- Repeat the tests (PID_tuning program) and compare the curves.
Common pitfalls
- P too high → vibrations, noise, overcorrections.
- I too high → slow response + slow oscillations (windup).
- D too high → sluggish response, noticeable delay.
Practical tips
- Keep a log of tested values (P, I, D) + screenshots of the curves.
- Always test with the same sequence of angles/speed to compare accurately.
- Payload and friction influence tuning → adjust the gains accordingly.
Restore factory parameters
If needed, you can restore the default PID parameters provided by the manufacturer to return to a stable baseline behavior.